Hace poco se ha celebrado en Madrid el llamado Congreso Internacional de Matemáticos o ICM, y se ha hablado mucho de un matemático llamado Grigori Perelman que ha resuelto uno de los grandes problemas abiertos de las matemáticas, la conjetura de Poincaré. Entre otras cosas, se ha dicho que esta conjetura ayudará a conocer la verdadera forma del Universo. El caso es que en ninguna parte han tratado de profundizar un poco más ni en la ciencia matemática a la que pertenece dicha conjetura, la topología, ni en cómo exactamente va a ayudar a semejante prodigio de la astrofísica, y por eso me he liado la manta a la cabeza y he decidido (intentar) explicarlo siendo lo más claro posible, pero tampoco simplista. Así que vamos allá. En este primer artículo voy a hablar un poco de la topología y a lo que se dedica.
Lo primero de todo: la topología NO tiene nada que ver con la topografía, un error bastante habitual. La topología es una rama de la geometría que tiene como objetivo clasificar todas las formas existentes. Así de fácil y así de complejo. De ese modo, al conocerse todas, se podría ayudar a muchas otras ciencias a la hora de establecer modelos aproximados de la realidad, y en especial a la física.
Lo primero que hace la topología es tener en cuenta el asunto de las dimensiones de los objetos, desde una sola dimensión hasta las que uno quiera (no hay límite en términos abstractos). Es importante no confundir la dimensión de un objeto con la del espacio que lo contiene. Por ejemplo, una pelota tiene dimensión dos, aunque está dentro del espacio tridimensional. ¿Y por qué es esto? Pues porque si fuéramos un bicho y estuviéramos apoyados en la pelota para nosotros no sería muy distinto de un plano. Fijado un punto de partida, con dos números (latitud y longitud) nos bastaría para desplazarnos, igual que en un plano nos bastaría con saber cuándo a la derecha o izquierda y cuando arriba o abajo nos desplazamos del origen. Por otro lado, un muelle posee una sola dimensión, porque por el mismo motivo, viviendo dentro de él no notaríamos diferencia entre él y un alambre recto.
Vamos a llamar a los objetos de dimensión dos superficies (porque en verdad lo son).
Por fortuna hay métodos indirectos para poder distinguir unos objetos de otros. Del mismo modo que nosotros no necesitamos salir de la Tierra para saber que es redonda, ciertas evidencias físicas como la gravedad o el concepto de curvatura y las longitudes de las sombras nos darían pistas para saber cómo es una superficie en la que estamos atrapados.
Claro, alguien puede decir, pues para qué eso si podemos verlo desde fuera. Eso está muy bien si hablamos de superficies, pero hemos dicho que la topología se encarga de todas las dimensiones. Pensemos en dimensión tres. Igual que hay muchas clases de superficies, hay muchas clases de objetos de dimensión tres, aunque no los podamos percibir. De hecho, vivimos dentro de uno muy grande del que parece que no podemos escapar: el Universo. Así que enfocar el estudio de estas formas desde el punto de vista anterior no es una tontería, ni mucho menos.
De modo que nos centraremos en las superficies. Salvo algunas pocas excepciones de objetos unidimensionales (como por ejemplo un hilo), en nuestra vida cotidiana todo lo que nos rodea son superficies. Claro, así a priori pensar en clasificar todas esas formas parece una tarea titánica. Y en verdad lo es, además de un poco innecesaria, porque en el fondo hay formas que no son tan distintas de otras. Es por ese motivo que los topólogos, para hacerse la vida un poco menos imposible, decidieron que si podíamos coger una superficie y deformarla hasta obtener otra, entonces eran esencialmente iguales. Por ejemplo, todas las pelotas, con independencia de su radio, son iguales, porque podemos estirarlas o aplastarlas hasta tener las otras. Y no sólo eso, de hecho un balón de rugby es igual a una pelota, e incluso una cuchara es igual a una pelota. Imaginen que la cuchara es de plastilina, por tanto la pueden deformar todo lo que quieran mientras no corten ni peguen nada hasta hacer una pelota con ella. Pero por ejemplo, un donut nunca será igual a una esfera, porque por mucho que deformen, no podrán librarse del agujero del medio (por eso es importante la regla de no pegar ni cortar).
Bueno, la clasificación es ahora un poco más sencilla… ¿o no? Pues aunque parece que hemos simplificado muchísimo, aún existen demasiadas formas. De modo que vamos a pedir algo más, dos propiedades un poco extrañas pero que dan coherencia a todo el asunto.
La primera es que los objetos serán compactos. La idea de un objeto compacto es que aunque no esté acotado, posee propiedades y ventajas parecidas. Eso se consigue poniendo una serie de propiedades matemáticas que no vienen al caso, y es razonable porque los objetos no compactos de dos dimensiones son muy escasos en la naturaleza.
Por otro lado vamos a pedir que no tengan borde. Por borde se entienden finales bruscos, como las esquinas de un cubo o la base de un cono. El motivo de eso es que con nuestro truco de deformar podemos hacer suaves esos bordes, de modo que considerar objetos con borde no haría más que complicar las cosas.
Vamos mejor. Esto ya empieza a tener buena pinta. Ahora presentaré una serie de superficies importantes en el mundo de la topología. La primera de ellas ya la conocen. Es la esfera.
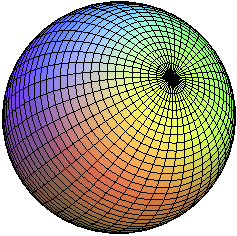
La esfera es una superficie muy importante. Para empezar, porque con nuestro truco de deformar, hay millones de cosas que pasan a tener la misma forma de una esfera. Sólo en mi escritorio cuento así en un momento un par de docenas (eso sin incluir todos y cada uno de mis bolígrafos y lapiceros).
El siguiente en la lista hay sido mencionada antes bajo la forma de donut. Su nombre matemático es el toro.
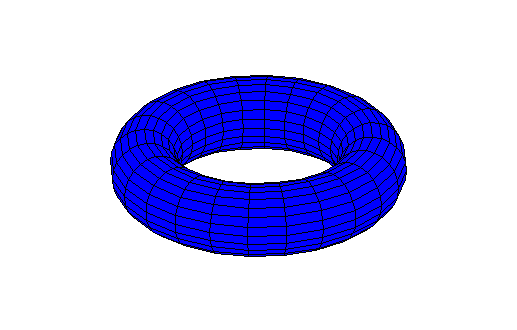
Es importante destacar del toro que, como decía antes, tiene entidad propia, no es como la esfera. El toro es el gran representante de todos los objetos con un agujero que conocemos, como una taza de café. El agujero hace que, por ejemplo, dos viajeros, uno que siga un círculo vertical, y otro que siga un círculo horizontal, no puedan jamás encontrarse salvo al regresar de nuevo al punto de partida (no como en la esfera, donde sus rutas se cruzan en las antípodas).
Otra cosa importante del toro es que hay una manera de dibujarlo en dos dimensiones, y es como si fuera una especie de recortable. Cogemos un cuadrado (que si es necesario podemos estirar como chicle en vertical ú horizontal, recuerden), y pegamos los lados opuestos entre sí teniendo en cuenta que las puntas de las flechas deben coincidir:
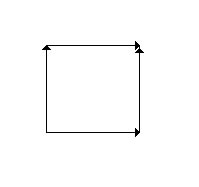
¿Por qué es importante (y mucho) esto? Porque podemos estudiar una superficie usando sólo dibujos planos. Si un bichito que viviera en una pelota de tenis evolucionara mucho, podría hacerlo, de hecho, aunque no tuviera percepción de la tercera dimensión. Y volviendo al Universo, nosotros apenas tenemos percepción de la cuarta dimensión, pero gracias a este procedimiento, podemos ver el Universo a partir de un esquema de recortables parecido a éste. Claro, es más complicado porque ahora las cosas que se juntan no son líneas sino superficies y en teoría no partimos de un cuadrado sino de un cubo, pero la idea básica se mantiene.
Pero vamos a regresar al cuadrado. A base de poner distintas flechas uno puede jugar una barbaridad y obtener formas de lo más variopintas. Incluyendo una nueva regla, que es que los lados opuestos sin flechas no se deben pegar, vamos a poner unos ejemplos a ver si son capaces de distinguir de qué figuras hablamos:
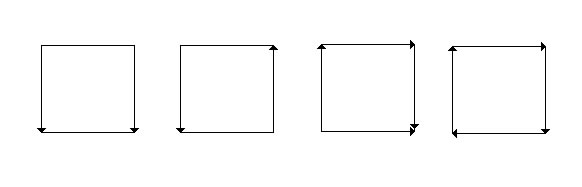
La primera, en efecto, es un cilindro, pues es como coger una tira de papel y pegarla por los extremos. La segunda, sin embargo, al tener las flechas apuntando al revés, da otra forma ligeramente distinta. La idea es que antes de pegar los extremos de nuestra tira damos un giro. Esta superficie, que seguro a muchos les suena porque la ciencia ficción la adora, es la banda de Moebius (no confundir, por cierto, con el por otro lado magnífico dibujante).

La banda de Moebius tiene una extraña propiedad: no posee nada que se pueda llamar dentro y fuera. A un cilindro, con poner dos tapas, le basta para poseer interior y exterior. Un toro y una esfera, evidentemente, lo poseen. Pero cualquier intento de hacer eso con la banda de Moebius está destinado al fracaso. De hecho, si uno se pone a andar por la cara interior de la banda, de repente aparece por la cara exterior y viceversa. Ojalá pasara eso con una esfera, en concreto con nuestro planeta (es decir, que viajando por el exterior que de repente apareciéramos en el interior). Esta propiedad se llama ser no orientable, y la banda de Moebius no es la única superficie que la posee. Los dos últimos cuadrados tampoco lo son. Es posible que algunos se hayan roto la cabeza intentando imaginar qué formas tienen. No se esfuercen, no se pueden concebir por la mente humana con claridad de lo extraños que son porque no pueden ser dibujados en un espacio de dimensión tres. El primero de ellos se llama la Botella de Klein, y el dibujo que mejor lo aproxima es el siguiente:
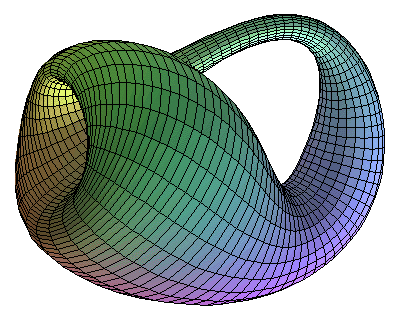
Es una superficie muy rara pero muy importante, la idea es que la botella tiene conectado el cuello y la base y está a la vez dentro y fuera de sí misma, pero esto es sólo una manera de hablar, porque como la banda de Moebius, no posee dentro ni fuera. La otra se llama el plano proyectivo. La representación del cuadrado de arriba no es la más habitual para referirse a ella. Se usa mucho en dibujo técnico y en perspectivas, porque en ella no existen las rectas paralelas (de hecho, se puede decir que su inventor es Leonardo Da Vinci).
Sólo me falta un ingrediente para la gran receta, y es la suma conexa de dos superficies. La idea de la suma conexa es: cogemos un tubo, pegamos un extremo a una superficie, otro a la otra, y tenemos una suma conexa. Como podemos deformar lo que queramos, al final es como si cosiéramos una superficie a otra, en cierto modo. Así que vamos a ver, la suma conexa de un toro y una esfera es… un toro con un bulto redondo enorme, ¿no? Peeero, deformamos el bulto enorme (imaginen que es como un grumo de harina que hundimos) y tenemos… pues otra vez el toro. Ahora, la suma conexa de dos toros es… pues es una figura nueva. Tener dos agujeros no tiene nada que ver con tener uno ni tener ninguno. Esta figura se llama, como es lógico, el ocho. Es representante de objetos de la vida cotidiana con dos agujeros, como unas tijeras.
Y por fin, llega la gran clasificación. Vale, vale, vale, tenemos una superficie cualquiera, que es compacta y sin borde, acordamos. Entonces:
- Si es orientable, es o una esfera, o un toro, o sumas conexas de varios toros entre sí (tres agujeros, cuatro, cinco…)
- Si no lo es, o es el plano proyectivo, o es la Botella de Klein, o es sumas conexas de estas dos superficies (aquí podemos mezclar, y salen cosas distintas, no como arriba, que coser una esfera no vale para nada).
Y ya está. Se acabó. No hay más. De este modo se obtienen TODAS las superficies que existen en el Universo. Si ya quieren ser más precisos, empiezan a deformar y punto, pero tampoco es necesario, porque la geometría de dos superficies, si una es deformada a partir de la otra, posee la misma naturaleza. De modo que ahora conocen todas las formas esenciales de todas las superficies del Universo. Bueno, este resultado, por supuesto, es difícil de demostrar, mucho.
Por desgracia, no se ha conseguido este resultado en las superficies de tres dimensiones, es decir, no sólo es que no sepamos qué forma tiene el Universo, es que ni sabemos con seguridad todas las posibilidades. Pero aun así, existen ciertas cosas que debería cumplir. Por otro lado, el reciente descubrimiento de Perelman ha ayudado a que haya que buscar menos formas. Pero todo esto, en la segunda parte de este artículo.
por Miguel Angel López
(Para más detalles leer el artículo La Forma del Universo, por Vicente Muñoz).